こんにちは、コンスキです。
4ビットの2進数で表せる範囲の数字同士の乗算をブースのアルゴリズムを使ってやる方法を紹介します。
今回は、3×(-4)の計算を実際にやってみたいと思います。
2進数に変換する
計算する2つの値が10進数の場合は2進数に変換します。
3x(-4)の場合は、3がかけられる数で被乗数と呼ばれ、-4がかける数で乗数と呼ばれます。
被乗数と乗数を2の補数表現で表した4ビットの2進数に変換します。
3 → (0011)2 -4 → (1100)2
被乗数に関しては、符号を変えたものを4ビットの2進数に変換します
3 → -3 → (1101)2
表を書く
ブースの乗算アルゴリズムで計算する上で表を使います。
被乗数のビット数をx、乗数のビット数をyとします。
1 .3行(x+y+2)列の表を書きます。今回は乗数も被乗数も4ビットであるため、3行10列の表を書きます。
2. 1列目の各行にラベルをつけます。
| A | |||||||||
| S | |||||||||
| P0 |
A・・・add(加算)の頭文字 S・・・subtract(減算)の頭文字 P・・・product(積)の頭文字
3. 1行目に被乗数を左詰めで入れます。
| A | 0 | 0 | 1 | 1 | |||||
| S | |||||||||
| P0 |
4.2行目に被乗数の符号を変えたものを左詰めで入れます。
| A | 0 | 0 | 1 | 1 | |||||
| S | 1 | 1 | 0 | 1 | |||||
| P0 |
5.3行目に乗数を入れます。この時、右側を1ビット空けるようにして入れます。
| A | 0 | 0 | 1 | 1 | |||||
| S | 1 | 1 | 0 | 1 | |||||
| P0 | 1 | 1 | 0 | 0 | 空ける |
6.空いているマスに0を入れます。
| A | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| S | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| P0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
7.Pyのラベルまで行を増やします。今回は4ビットであるためP4までです。
| A | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| S | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| P0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| P1 | |||||||||
| P2 | |||||||||
| P3 | |||||||||
| P4 |
P0からP3までが途中の計算結果を入れておく行で、P 4が最終的な積が入る行になります。
計算する
ここからが計算する部分です。
計算の手順としては次のようになります。
Pの行の末尾2ビットを見る ▶︎ 条件に照らし合わせる ▶︎ 操作する
条件と操作
Pの行末尾2ビットを見て、それに応じて次のような操作をします。
| 末尾2ビット | 操作 |
|---|---|
| 00、11 | 何もしないで右シフトする |
| 01 | PにAの行を足してから右シフトする |
| 10 | PにSの行を足してから右シフトする |
それでは3×(-4)を実際に計算していきます。
P0の行の末尾2ビットを見ます。
| A | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| S | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| P0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| P1 | |||||||||
| P2 | |||||||||
| P3 | |||||||||
| P4 |
末尾2ビットは「00」であるため、何もせずに右シフトします。

操作をしたら、この数を下の行に入れます。
| A | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| S | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| P0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| P1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| P2 | |||||||||
| P3 | |||||||||
| P4 |
今度はP1の行の末尾2ビットを見て操作します。
| A | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| S | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| P0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| P1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| P2 | |||||||||
| P3 | |||||||||
| P4 |
末尾2ビットは「00」であるため、何もしないで右シフトします。

それをP2 の行に入れます。
| A | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| S | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| P0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| P1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| P2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| P3 | |||||||||
| P4 |
今度はP2の行の末尾2ビットを確認します。
| A | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| S | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| P0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| P1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| P2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| P3 | |||||||||
| P4 |
末尾2ビットは「10」であるため、P2の行にSの行を足します。

その後、右シフトします。

この数をP3に入れます。
| A | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| S | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| P0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| P1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| P2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| P3 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| P4 |
今度は、P3の行の末尾2ビットを見ます。
| A | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| S | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| P0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| P1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| P2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| P3 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| P4 |
末尾2ビットは「11」です。
そのため、何もせずに右シフトします。

その後、この数をP4の行に入れます。
| A | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| S | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| P0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| P1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| P2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| P3 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| P4 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
計算はこれで終わりです。
P4の行の一番右のビットを削除します。

これが3×(-4)の2進数での答えになっています。
答えの確認
先ほど計算で導き出した「(11110100)2」が本当に答えになっているのか確かめてみます。
10進数に直すと…
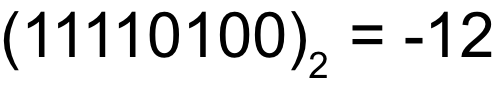
3×(-4)の答えも-12になるので、合っていますね!




コメント
[…] […]