「10進数をIEEE754単精度で表現せよ」という問題の解き方

こんにちは、コンスキです。

「10進数をIEEE754単精度で表現せよ」もしくは、「10進数をIEEE754単精度に変換せよ」という問題の解き方をご紹介します。

今回は例として、-85.125という10進数をIEEE754単精度で表現する過程を取り上げてみます。

浮動小数点数表示の構成（32ビット）

0か1が入る1桁のことを1ビットと呼びます。

32ビットの浮動小数点表示は、次のような構成になります。

なぜこの構成になっているのか、最初は謎ですよね。

1度解いてみましょう。なんとなく分かると思います！

大まかな解き方

大まかな計算手順は次の3ステップです。

詳しい解き方

例として、-85.125という10進数をIEEE754単精度で表現していきます。

手順1. 仮数部の符号を求める

仮数部の符号は、10進数が正なら「0」で、負なら「1」です。

-85.125は負であるため、仮数部の符号は「1」になります。

手順2. 指数部eを求める

まず、10進数を2進数にします。

10進数に「-（マイナス）」が付いている場合は、「-」を取った後に2進数にします。

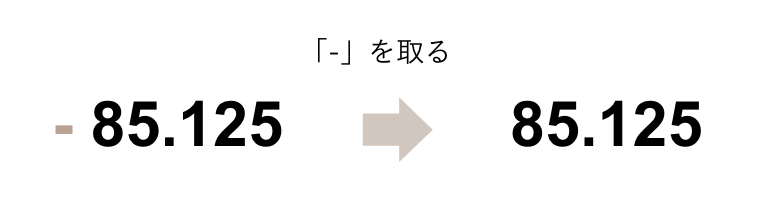
整数部分から2進数にします。

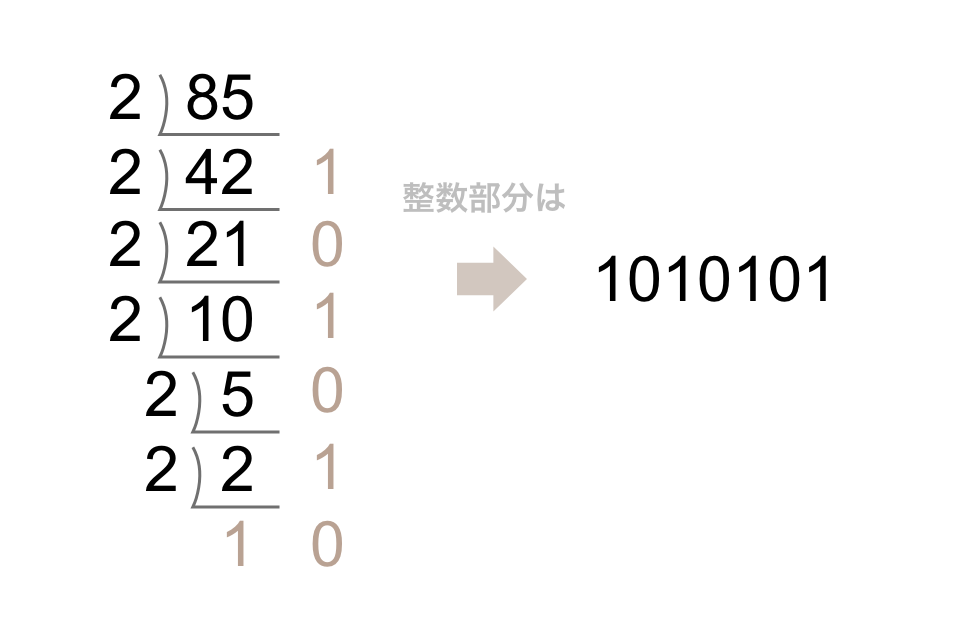
次に小数点以下を2進数にします。

整数部分と小数点以下を合体します。

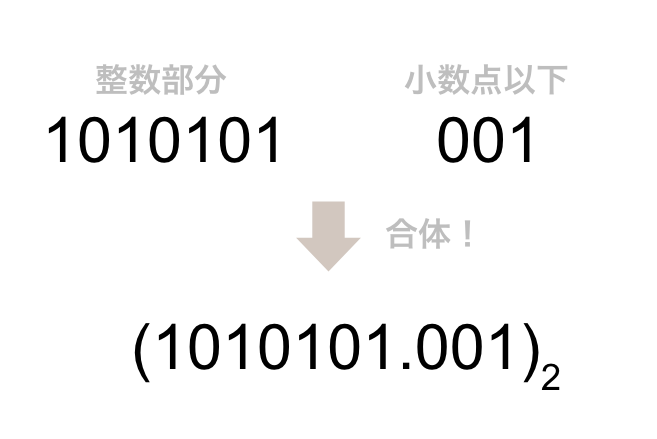
その2進数を正規化します。（正規化:111を1.11×2²に直すような作業）

2の右肩にある数字に、バイアス値の127を足した値を求めます。

この133を2進数にします。

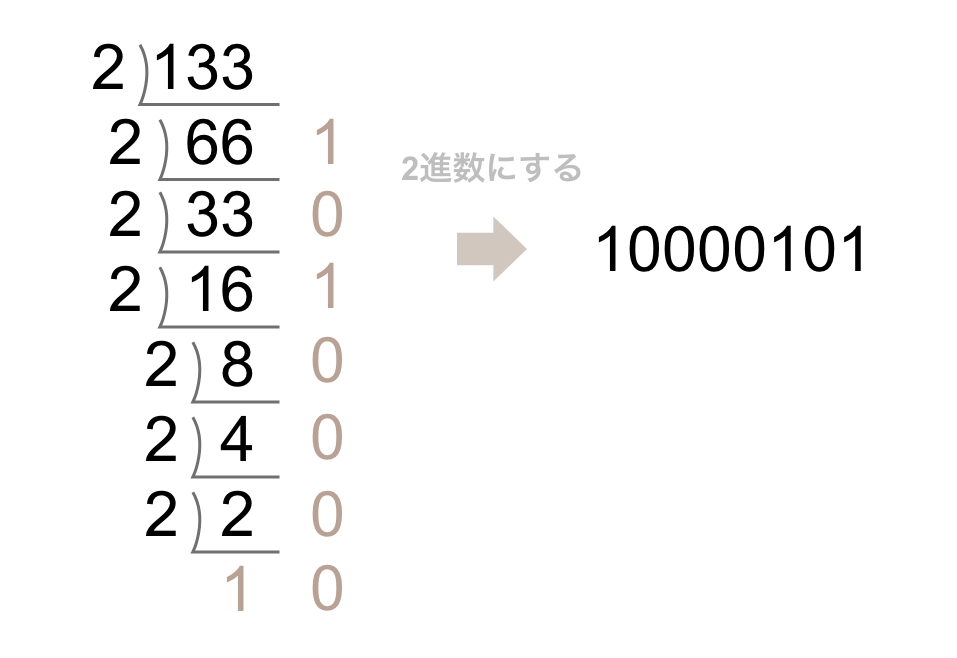
この「10000101」が指数部eです。

手順3. 仮数部mを求める

先ほどの正規化した2進数に注目します。

小数点とその左にある1、そして×2^Eの部分を省略します。

この「010101001」を仮数部に入れます。

この時、左側に詰めて入れることに注意してください。

仮数部の空いている部分に0を入れます。

これが10進数をIEEE754単精度で表現したものになっています。

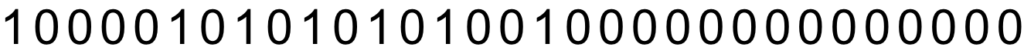
最後に

「10進数をIEEE754単精度で表現せよ」もしくは、「10進数をIEEE754単精度に変換せよ」という問題は解けましたか？

この記事が問題を解く助けになったらうれしいです。

ここまで読んでくれてありがとうございました。